The Biomechanics of Swimming
John Merck
The biomechanics of swimming boil down to two major concepts:
- Streamlining: optimization of form for reduction of drag.
- Displacement: ability to move water so that it will function as reaction mass for propulsion.
Drag: the resistance to movement of a body through a fluid, occurs in two varieties:
- Form drag: resistance due to cross-sectional area of the body - the profile that it presents to oncoming water.
- Frictional drag: resistance occurring where the surface of body meets fluid - function of:
- fluid viscosity
- surface area.
The relationship of form and frictional drag is represented by the
Reynolds Number:
Reynolds Number = Re = 2rVρ/μ
Where:
- r is the hydraulic radius ((2A/P) where A = cross-sectional area and P = wetted perimeter)
- V is the flow velocity (m/s)
- ρ is the fluid density (kg/m3)
- μ is viscocity (kg/(m.s)).
Note: The numerator shows inertial forces, or the tendency of discrete particles of fluid to resist changes in velocity and continue to move uniformly in the same direction.
The denominator - viscosity, or resistivity to shearing or deformation. For our purposes, we can simplify to:
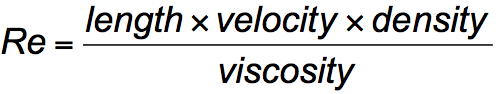
Easy to calculate, but where, exactly, are form and friction drag represented?

Since density & viscosity are essentially constant within an environment, they essentially cancel out, leaving:
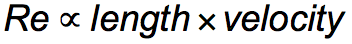
Ultimately, the Reynolds number addresses the behavior of the boundary layer that surrounds an object moving through a viscous fluid. That layer is influenced by the viscosity of the fluid and the speed of the object.
Consider the familiar example of raindrops on a moving car:
- At low speed, raindrops roll downhill on the windshield under the influence of gravity. They can do this because the vehicle is operating at a low Reynolds number so its boundary layer is thick enough completely to encompass the raindrops.
- At higher speeds (and higher Reynolds numbers), the raindrops begin to move upward because the boundary layer has become thin enough that the drops are poking out of it and being blown by the surrounding medium.
- At very high speeds (don't try this at home) the drops move in random directions because the boundary layer is now so thin that the currents of the surrounding medium are channelled through minor irregularities of the windshield's topography (scratches, half-cleaned bird-shit stains, etc.)

Of course, the faster the car goes, the thinner the boundary layer gets and the more things poke out of it. When they do, they cause frictional drag in the surrounding medium. SO... objects operating at higher Reynolds numbers inherently experience more frictional drag than objects at lower Reynolds numbers.
As a first order approximation, the Reynolds number in water is a function of velocity and length. So.....
Large or speedy swimmers operating at higher Reynolds numbers (greater than 10,000) have a greater need for streamlining than smaller or slower ones operating at lower values (less than 100). E.G.:
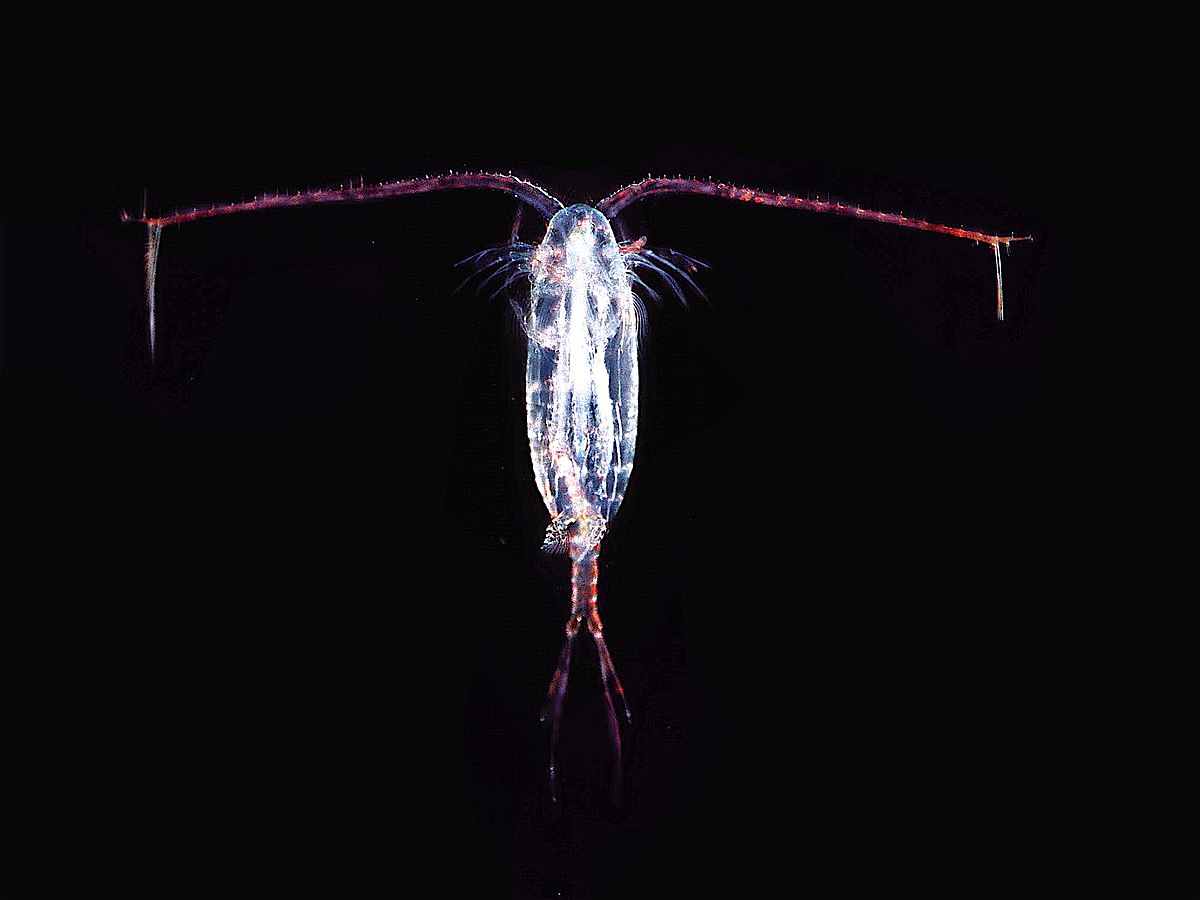
- Copepod: lives within its boundary layer, experiences little frictional drag, and has no need for significant streamlining.
- Chetognath: Although small, so still operating at relatively low Reynolds numbers, moves fast enough that it benefits from streamlining.
- jack: a medium-sized (40 - 100 cm) high speed predator. Operates at moderate Reynolds numbers.
- tuna: A large (2 -m) high-speed apex predator operating at high Reynolds numbers. Absolutely needs to be well streamlined.
- whale shark: Large enough that it operates at high Reynolds numbers all the time. Although a suspension feeder that can easily outrun its prey, it must be highly streamlined to swim efficiently at any speed.
Accelerating reaction mass:
But how do we accelerate an animal to the point that we need to think about Reynolds numbers in the first place? By water displacement. All swimmers use displaced water as a reaction mass to move their bodies forward (Newton's third law of motion.) This happens in three general ways:- Recoil locomotion: Water, held in a body cavity, is forcibly expelled through an aperture. (Not in vertebrates)
- Appendicular locomotion: Water is displaced to the rear by an appendage
- Axial locomotion: Water is displaced to the rear by movements of the body axis.
Appendicular locomotion
Appendages are used to displace water. This takes two general forms:
- Rowing: In which the form drag that the appendage experiences when it is moved backwards entrains a mass of water.
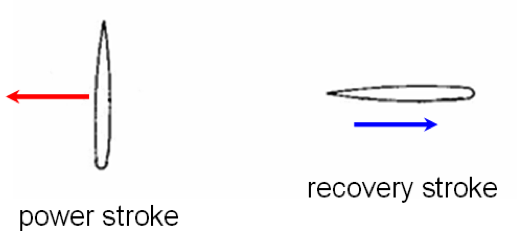
Examples:
- Crab
- pond turtle
- Grebe
- butterfly fish (pectoral fins)
Typically, rowing appendages emphasize area over shape, and are not distinctly tapered. The limb excursion involves a distinct power stroke where the maximum profile is presented to the water, and recovery stroke, where that profile is minimized by the folding or feathering of the limb.
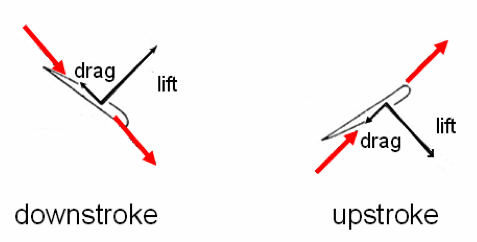
- Subaqueous flight: Where the movement of the appendage generates lift, pulling it forward. Note, lift occurs when a fluid moves without turbulence over upper and lower surfaces of a planar structure at different speeds, creating a region of relatively low pressure on the upper surface. This typically happens when the upper surface is more curved than the lower.
An interesting side effect, in aircraft design, is the tendency of vortices to form at wingtips, as air rushes from below into the low-pressure region above the wing. This renders the area near the wingtip useless for lift generation. Aircraft designers have developed wingtip winglets as a means of preventing these vortices. Subaqueous fliers typically approach the problem with swimming appendages that taper to a narrow point.
Examples:
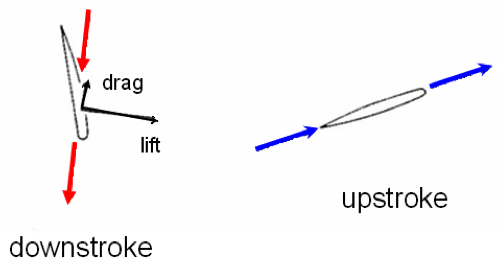
In principle, lift can be generated on either the up or downstroke of the appendage, however in life many organisms emphasize or completely rely on the downstroke. Thus, there is a continuum from symmetrical to highly asymmetrical subaqueous flight.
NOTE: Lift only becomes effective at higher Reynolds numbers, so slower/smaller swimmers favor rowing. We call it "flight" because actual flying animals operating at much higher Reynolds numbers use the same method.
Axial locomotion
Many creatures, especially chordates, use the sides of their torso to displace water during axial undulations in which the body is thrown into a series of S-curves that propagate rearward. If living primitive chordates like Branchiostoma, hagfish, and lampreys are any guide, the ancestral chordate's body was probably long and sinuous, and most of it was used in propulsion. From this ancestral state, axial locomotion has been variously derived in vertebrates.
Three major trends are apparent with increasing Reynold's numbers:
- Immobilization of the anterior torso
- the reduction of the undulating length.
- Increasing height of the caudal fin
- Angilliform:
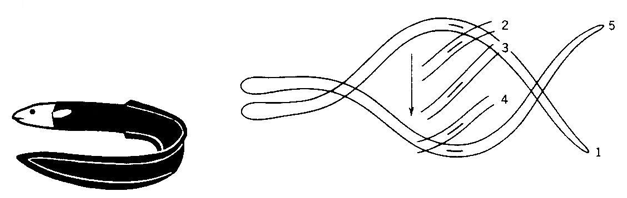
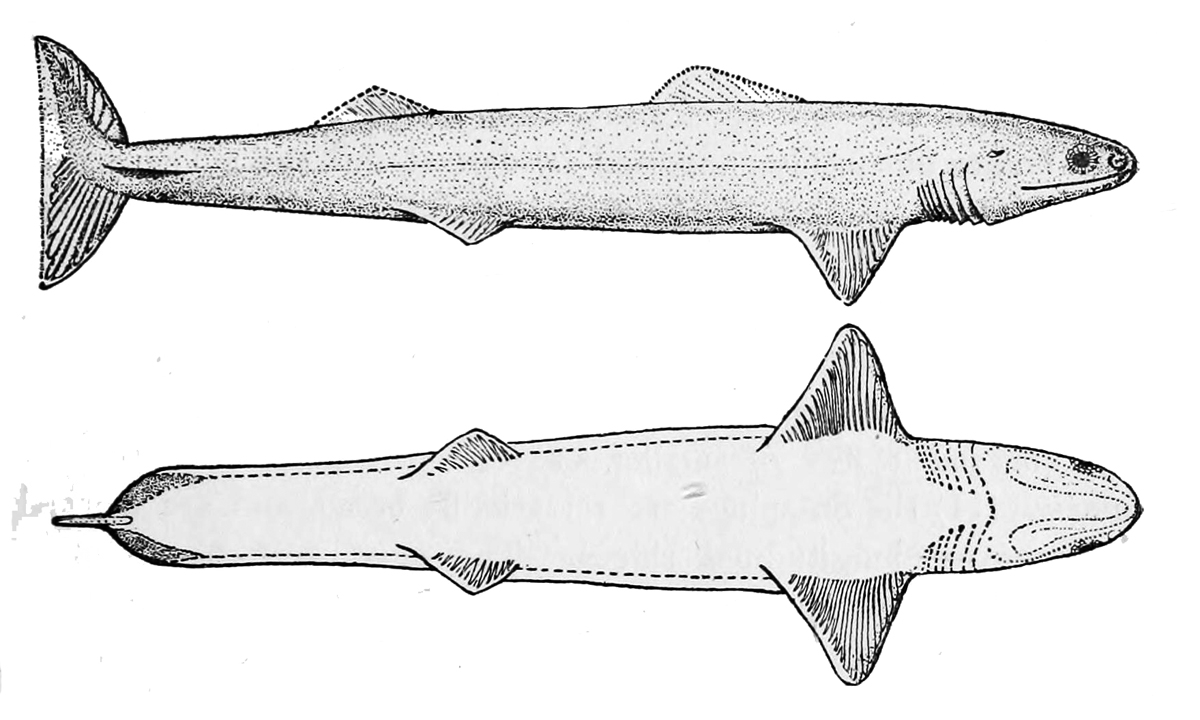
The ancestral craniate shape. Lond and sinuous with most of the torso contributing to propulsion. The elongate shape increases the Reynolds number at which the creature operates, while the high SA/V ratio increases frictional drag. Thus, angilliform swimmers typically operate at lower speeds. Example: hagfish

- Carangiform: The body is more compact and stiff. Lateral undulations are limited to the posterior half, with a distinct caudal (tail) fin increasing the propulsive surface area without adding significantly to mass or cross-sectional area. Example: koi
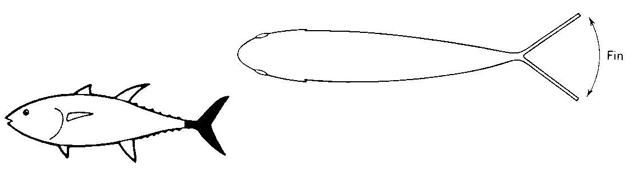
- Thunniform: Lateral movement of the torso is limited to the caudal peduncle (tail) and fin. The caudal fin is semilunate - i.e. tall and half-moon shaped.
In thunniform swimmers, water displacement is achieved by lift, generated by the caudal fin, rather than drag. The caudal fin has a high aspect ratio (span of fin/chord). Because lift is more efficient at higher speeds and Reynolds numbers, the thunniform morph is optimized for high absolute speed. The body must be highly streamlined. Indeed, even the caudal peduncle, the source of drag displacement in slower swimmers, is streamlined to reduce drag in its side-to-side motion. The strong selection for streamlining results in a typical maximum fineness ratio (diameter/length) of .25 at about 1/3 of the body's length. Example tuna.
A second trend - accelerators: Deepening and lateral compression of the body for acceleration. Many vertebrates operate at low Reynolds numbers but need to be able to accelerate quickly. In these, the depth of the torso increases to facilitate the rapid displacement of larger volumes of water without increasing length and Reynolds number. This morph, optimized for rapid acceleration at low absolute speeds, is typical of:
- Lurking predators. Example: pike.
- creatures that typically defend a territory but must be able to escape quickly, such as reef fish. Example: King angelfish.
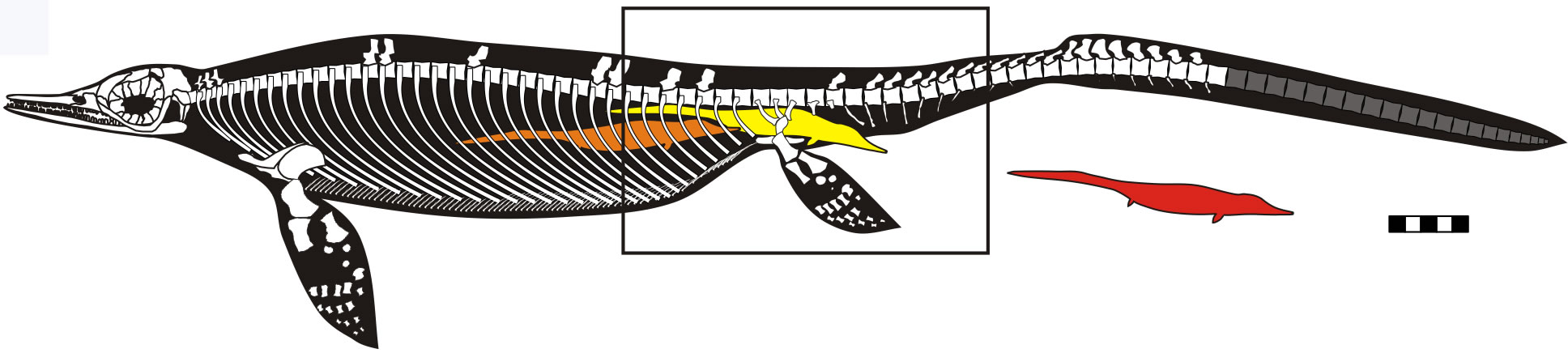
The biomechanical constraints of swimming give us robust criteria for rejecting hypotheses of ancient creatures' life habits.
Eusthenopteron foordi